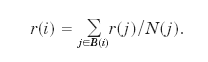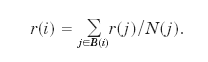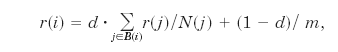PageRank Module
Introduction:
PageRank is a global ranking system
that tries to capture the
importance of pages in the world wide Web.
The Web is very
large, with great variation in the amount, quality and
the type of information in Web pages.
Also many Web
pages are not sufficiently self-descriptive. Hence
traditional information retrieval (IR) techniques are not effective
enough in capturing importance of a page.
The link structure
of the Web contains important implied information,
and can help in filtering or ranking Web pages. In particular, a link
from page A to page B can be considered a recommendation of page B by
the author of page A. Many algorithms have been proposed to exploit the
link structure, like HITS (Hyper Text Induced Topic Search) by
Kleinberg[1999], PageRank by Page et al [1998] and Citation Ranking.
Background:
PageRank ranks a page taking into
consideration the number of
pages that point to a given page and the importance of that pages.
Let the pages on
the Web be denoted by 1, 2, . . . , m. Let N(i) denote
the number of forward (outgoing) links from page i. Let B(i) denote the
set of pages that point to page i. For now, assume that the Web pages
form a strongly connected graph (every page can be reached from any
other page). We will relax this assumption shortly. The simple PageRank
of page i, denoted by r(i), is given by:
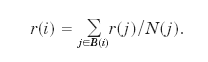
In linear algebra,
this can be written as r = ATr
, where r is the m x 1 vector [r(1), r(2), . . . , r(m)], and the
elements ai, j of the matrix A are given by, aij = 1 /N(i) , if page i points to page j, and ai,
j = 0 otherwise. Thus
the PageRank vector r is the
eigenvector of matrix AT
corresponding to the eigenvalue 1. Since the graph is strongly
connected, it can be shown that 1 is an eigenvalue of AT,
and the eigenvector r is
uniquely defined.
Design issues of PageRank:
1.Choosing a method:
One of the methods
for computing the principal eigenvector of a matrix is called Power Iteration. In power iteration,
an arbitrary initial vector is multiplied repeatedly with the given
matrix, until it converges to the principal eigenvector. Power
iteration is guaranteed to converge only if the graph is aperiodic. (A
strongly connected directed graph is aperiodic if the greatest common
divisor of the lengths of all closed walks is 1.) In practice, the Web
is always aperiodic.
2.Problems with PageRank Calculation:
Any strongly
(internally) connected cluster of pages within the Web graph from which
no links point outwards forms a Rank
Sink. An individual page that does not have any outlinks
constitutes a Rank Leak. In
case of a rank sink, nodes not in a sink receive a zero rank. On the
other hand, any rank reaching a rank leak is lost forever.
2a.Eliminating Rank Sink:
We plan to
introduce a decay factor d (0 < d < 1) in the PageRank
definition. In this modified definition, only a fraction d of the rank
of a page is distributed among the nodes that it points to. The
remaining rank is distributed equally among all the pages on the Web.
Thus, the modified PageRank is
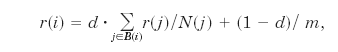
where m is the total number of
nodes in the graph.
2b.Eliminating
Rank Leak:
We are assuming
that leak nodes have links back to all the pages that point to them.
This way, leak nodes that are reachable via high-rank pages will have a
higher rank than leak nodes reachable through unimportant pages.
3.Convergence of algorithm:
In order for the
Power Iteration to be practical, it is not only necessary that it
converge to the PageRank, but that it does so in a few iterations. The
convergence of the Power Iteration for a matrix depends on the
eigenvalue gap, which is defined as the difference between the modulus
of the two largest eigenvalues of the given matrix. Page et al. [1998]
claim that this is indeed the case, and that the Power Iteration
converges reasonably fast (in around 100 iterations).
Arasu et al.
[2002] made a quantitative study of various iterative techniques and
found out that Gauss Seidel
method converges
faster than Power iteration and Jacobian method. We plan to implement
this method also to verify their claim.
4.Reducing
iterations in algorithm:
Since we are only interested in the relative ordering of the pages
induced by the PageRank than the actual PageRank values themselves, we
plan to terminate the power iteration once the ordering of the pages
becomes reasonably stable.
5.Robustness against spamming:
Since PageRank
is a global ranking algorithm it is relatively robust to spamming. Also
we plan to put a limit on the number of links that point to a given
page within the same domain to reduce spamming.
6.Improving Perfromance:
We will be implementing the code in perl. We also plan to
profile the program so as to identify snippets of code that take more
time. The performance of these can be improved either by changing the
datastructures or by
'caching'. In
perl we have a module
'Memoize'
that can be used to cache the return value of a function. If the
function is called again in a short span of time without change in
arguments, then the cached value is returned.
Data Structures Needed:
Inputs Required from the Storage
Module:
For calculating pagerank, we must have information about each link
between two pages . This information will be provided by stroage group
in the following form:
Page-id
No_Links Pageids
(source)
(destinations)
For
Example a typical entry is
N
5
BCDEF
where
N,B,C,D,E
and F are 8 byte pageids.
Data Structures and Functions Used:
Node of a
Graph:
sub new {
my $this = {
vertices => {},
in_edges => {},
rank => {}
};
bless $this, "graph";
}
Backlinks are stored per page
using the page identifier as a hash key and we insert them as elements
in
an anonymous array. This process is done in one pass, while scanning
the pageids
itself. Along with this we are also storing the number of outlinks per
page
using the same hash for that page identifier. The pagerank of each page
is also stored on a per element basis along
with the other attributes.
Add_Edge:
This function is called as each edge is inserted into the graph.
sub add_edge
{
# Edge from x to y
# If pageid x is seen for the first time,
# initialize its outdegree.
# Add the pageid x to an array associated with the pageid y as its backlink
}
In Edge:
This function returns the backlinks of a given page.
sub in_edge
{
# x is the given pageid.
# if x has backlinks,
# return the address of the array containing the backlinks.
# else return 0;
}
PageRank
Algorithm:
sub page_rank
{
# for each pageid do the following:
# get all the backlinks of that page
# calculate the contribution of all backlinks to the page rank
# of the current page.
# Their sum multiplied by damping factor '(1-d)' plus a threshold 'd'
# will determine the pagerank for this page.
# verify whether the newpageranks are close.. ie)within a threshold '€'
# of the previous pageranks.
# If so, exit..
# else repeat the Iteration
Performance Characteristics:
Let
us consider the number of pages to be ranked as 2,000,000.
Assuming
each document has around 30 links on an average, we require
8+4+8+8+30*8=268 bytes per page. For
2,000,000 pages it will be around 536MB. This will fit in memory in
either of the machines, Pushya
and Aaslesha which have 1GB
of main
memory each. We are planning to run this on either of these machines
for maximum efficiency.
Future Work:
1. The Power Iteration needs to be parallelized to scale for
ranking larger set of pages. We intend to do
this in future.
2. A variation of Power Iteration, the inverse Power iteration scales
well when parallelized, compared to
the original method. We also plan to implement this
in the fututre.